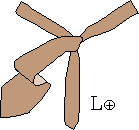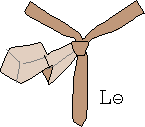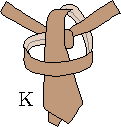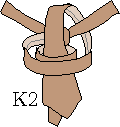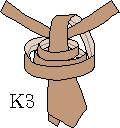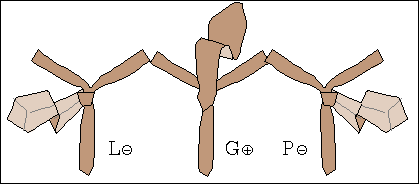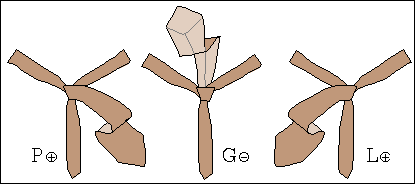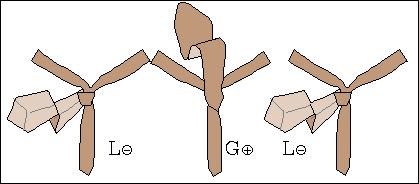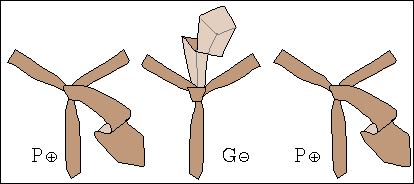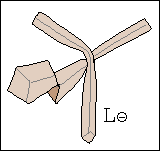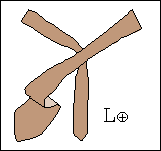1. Węzeł jako sekwencja stanów
*
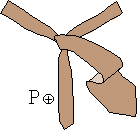
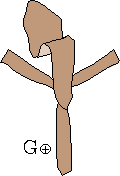
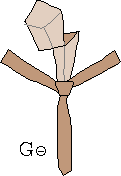
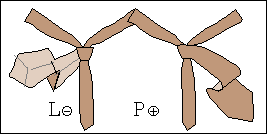
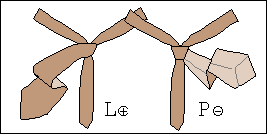
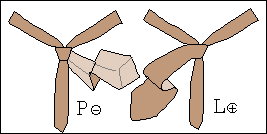
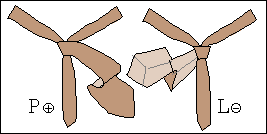
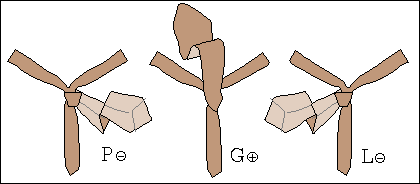
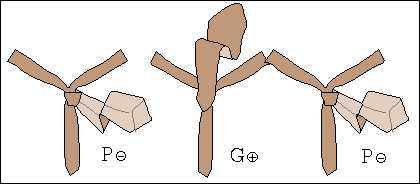
W procesie wiązania krawata można wyróżnić siedem stanów, rys. 1a, oznaczonych symbolami L⊕, L⊝, P⊕, P⊝, G⊕, G⊝ oraz K.
Litery L, P, G, K oznaczają "Lewo", "Prawo", "Góra" i "Koniec".
Znak ⊕ informuje natomiast, że wierzch krawata, tzn. wierzch jego szerszego końca jest widoczny, gdy stoimy przed lustrem.
Znak ⊝ mówi, że wierzch jest zwrócony jest ku koszuli i nie widzimy go w lustrze.
Stan K jest końcowy, krawat znajduje się w nim tylko raz, na zakończenie wiązania.
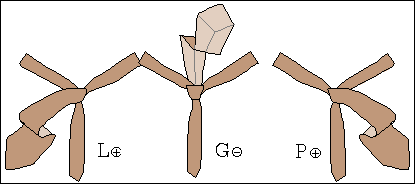
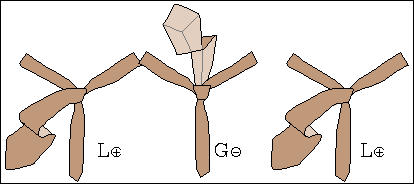
W niektórych węzłach wiązanie krawata można jednak zakończyć w nieco zmodyfikowany sposób, co pokazuje rys. 1b.
Można to zrobić, gdy podczas wiązania powstaną dwie lub trzy pętle.
Szerszy koniec krawata można bowiem przeciągnąć nie pod jedną petlą, lecz pod wszytkimi.
Stany takie oznaczono symbolami K2 i K3.
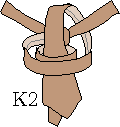
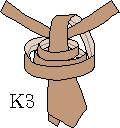
Rys. 1b. Zmodyfikowane stany końcowe
Wiązanie polega na przechodzeniu pomiędzy kolejnymi stanami w odpowiedniej kolejności.
Wykonuje się przy tym ruchy jedynie szerszym końcem krawata, krótszy pozostaje nieruchomy.
Przejście pomiędzy dwoma stanami np. od L⊕ do P⊝, co zapiszemy L⊕P⊝, nazywa się ruchem.
Węzeł równoważny jest zatem sekwencji stanów, przez które przechodzi krawat podczas wiązania, np.
L⊕G⊝P⊕L⊝G⊕P⊝L⊕G⊝K,
to windsor wiązany w ośmiu ruchach.
Natomiast
L⊕P⊝G⊕L⊝P⊕L⊝P⊕G⊝K2,
to christensen.
* W paragrafie tym wykorzystano prace:
T. Fink, Y. Mao, "Designing tie knots by random walk", Nature, vol. 398, str. 31-32, 1999.
T. Fink, Y. Mao, "Tie knots, random walks and topology", Physica A, vol. 276, str. 109-121, 2000.
T. Fink, Y. Mao, "85 sposobów wiązania krawata, czyli węzeł węzłowi nierówny", Media Rodzina, Poznań 2002.

2. Węzeł jako suma operacji
Wiązanie krawata można traktować także jako wykonywanie pewnych operacji w odpowiedniej kolejności. Wykonuje się cztery takie operacje, które oznaczymy jako O, S, S*, W.
Symbole te pochodzą od wyrazów "Obrót", "Środek" i "Węzeł orientalny". Omówimy je kolejno.
Operacja ½O, to półobrót, rys. 2, który polega na wykonaniu poziomego półobrotu szerszym końcem krawatu wokół cieńszego w jedną albo drugą stronę, tzn. z lewej na prawą lub z prawej na lewą. Jest to po prostu przełożenie szerszego końca krawata z jednego ramiena na drugie.
Można to wykonać nad cieńszym końcem, np. jak w ruchu L⊝P⊕, lub po nim jak np. w ruchu L⊕P⊝.
Mamy cztery takie półobroty, a mianowicie:
Operacja ta zajmuje jeden ruch.
Operacja S, to także przełożenie szerszego końca krawata z jednego ramienia na drugi, ale nieco dłuższą drogą - w dwóch ruchach,
patrz rys. 3. Krawat przechodzi bowiem przez pętlę pod brodą.
Operację taką można wykonać na cztery sposoby podane poniżej:
- L⊝G⊕P⊝,
- L⊕G⊝P⊕,
- P⊝G⊕L⊝,
- P⊕G⊝L⊕.
Operacja S, to dwa ruchy.
Operacja S*, rys. 4, jest pewną modyfikacją operacji S. Zaczynamy w niej jak w S, lecz wracamy na to samo ramię.
Operację tę można wykonać także na czery
sposoby, a to:
- L⊝G⊕L⊝,
- L⊕G⊝L⊕,
- P⊝G⊕P⊝,
- P⊕G⊝P⊕.
Jest ona wykonywana w dwóch ruchach.
Operację W, rys. 5, można wykonać na dwa sposoby, a mianowicie:
Operacja W jest także niezależnym, aczkolwiek najprostrzym, węzłem zwanym orientalny.
Niekiedy można ją wykonać w nieco zmodyfikowany sposób, np. L⊝P⊕G⊝K2, lub L⊝P⊕G⊝K3.
Zapisujemy ją wtedy jako, odpowiednio, W2, lub W3. Węzły, które kończą tymi operacjami nazywają się krzyżowymi. To takich należy np. wpomniany wcześniej christensen.
Operacja W, a także W2 oraz W3, zajmuje trzy ruchy.
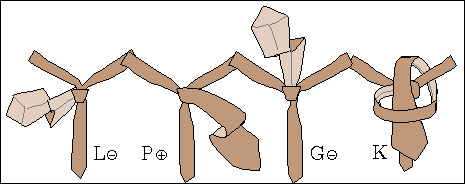

Rys. 5. Dwa sposoby wykonania operacji W
Opisane operacje można wykonywać kolejno jedna po drugiej, czyli dodawać.
Jeśli wykonamy bezpośrednio po sobie dwie operacje półobrotu w tę samą stronę, to całość tę zapiszemy jako ½O + ½O, co jest równoważne operacji O,
czyli pełnemu obrotowi. Zatem np. ½O + ½O + ½O = O + ½O = 1½O.
Podobnie możemy dodawać do siebie operacje S, co zapisujemy S + S = 2S, a także operacje S*, co wyrazimy pisząc S* + S* = 2S*.
Przy różnych operacjach kolejność wykonywania jest istotna, bowiem ½O + S ≠ S + ½O, ½O + S* ≠ S* + ½O oraz S + S* ≠ S* + S.
Operacja W jest szczególna, gdyż w każdym węźle występuje tylko raz, jako ostatnia.
Węzeł jest sumą operacji, np. wspomniany już windsor, patrz rys. 6,
L⊕G⊝P⊕L⊝G⊕P⊝L⊕G⊝K
wiązany w 8 ruchach zapisujemy teraz jako
S + ½O + S + W.
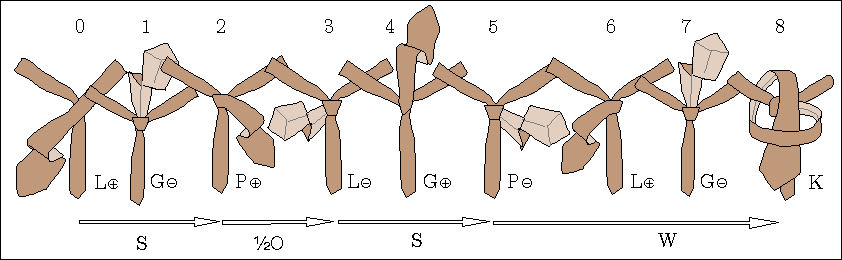
Rys. 6. Windsor, to L⊕G⊝P⊕L⊝G⊕P⊝L⊕G⊝K,
czyli S + ½O + S + W

3. Zasady obowiązujące przy wiązaniu
Przy wiązaniu krawata obowiązują trzy zasady:
- krawat zaczynamy wiązać układając go na jeden z dwóch sposobów, rys. 7, a mianowicie tak, że
- wierzch jest niewidoczny, co jest stanem L⊝ (węzły takie wiąże się w nieparzystej liczbie ruchów)
- wierzch jest widoczny, co jest stanem L⊕ (węzły takie wiąże się w parzystej liczbie ruchów),
- ruchy wykonujemy szerszym końcem, węższy pozostaje nieruchomy,
- każdy węzeł kończy się operacją W (czyli węzłem orientalnym, najprostrzym ze wszystkich).
Dzięki zasadzie nr 2, węzeł możemy łatwo rozluźnić, a następnie rozwiązać. Zasada nr 3 zapewnia, że to co otrzymamy jest właśnie węzłem krawatowym.
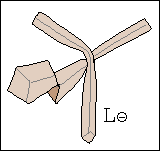
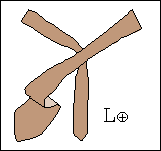
Rys. 7. Stany początkowe, L⊝ oraz L⊕

4. Węzeł jako spacer po kracie
Odłożymy na chwilę na bok operację S* i ustalimy węzły jakie można zawiązać przy pomocy operacji O, S i W.
Każdy z nich będzie głównym reprezentantem całej rodziny. Pozostałych jej członków otrzymuje się przez zastąpienie operacji S operacją S*.
Ograniczymy się przy tym do liczby ruchów nie większej niż 9.
Wiązanie węzła można teraz przyrównać do spaceru po kracie pokazanej na rys. 8.
Zaczynamy od dowolnego miejsca oznaczonego okręgiem. Poruszamy się jedynie w prawo lub do góry. Celem jest prawy, górny okrąg z wpisaną liczbą 3.
Ruch w prawo, to operacja ½O, do góry, to S.
Po dojściu do celu wykonujemy operację W, czyli wiążemy węzeł orientalny (w 3 ruchach, o czym informuje stosowna liczba w okręgu).
Poruszając się np. po ścieżce zaznaczonej kolorem czerwonym wykonujemy zatem kolejno operacje S, ½O, S i na końcu W.
Ścieżka ta odpowiada więc węzłowi
S + ½O + S + W,
czyli windsorowi, a dokładniej - reprezentantowi całej rodziny windsor.
Liczba 8 podana w okręgu, z którego wyszliśmy jest liczbą ruchów, w których wiąże się ten węzeł.
Liczba 3 obok tego okręgu informuje, że 3 różne ścieżki wychodzące od niego prowadzą do celu. Wychodząc od niego, można zatem zawiązać 3 różne węzły.
Oprócz windsora są to: 2S + ½O + W oraz ½O + 2S + W.
Na podobnej zasadzie, ścieżka niebieska, to 1½O + S + ½O + W, czyli główny przedstawiciel rodziny grantchester zawiązywany w 9 ruchach.
Widzimy więc, że każdą ścieżkę można utożsamić z odpowiednim węzłem.
Ogólnie zatem, liczba w każdym z okręgów oznacza liczbę ruchów, w których wiąże się węzły odpowiadające ścieżkom w nim się zaczynających.
Liczba obok okręgu oznacza liczbę wszystkich ścieżek prowadzących od niego do celu, czyli liczbę węzłów odpowiadających tym ścieżkom.
Każda taka ścieżka, wyznacza głównego reprezentanta całej rodziny.

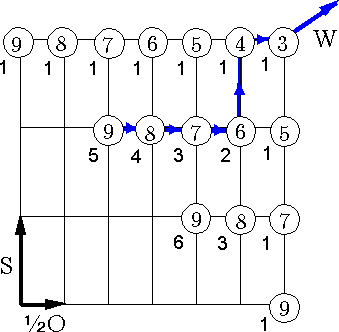
Rys. 8. Ścieżki na kracie odpowiadają węzłom.
Czerwona, to S + ½O + S + W, czyli winsdsor zawiązywany w 8 ruchach.
Niebieska, to 1½O + S + ½O + W, czyli grantchester zawiązywany w 9 ruchach.
Jest oczywiste, że w 3 ruchach można zawiązać jeden węzeł, podobnie w 4 ruchach.
W 5 ruchach można ich zawiązać 2, bowiem 1+1=2 (patrzymy na liczby obok okręgów, w których znajduje się liczba 5).
W sześciu - 3, bowiem 1+2=3 (teraz patrzymy na liczby obok okręgów, w których znajduje się liczba 6).
Wszystkich zatem węzłów, które można zawiązać w ten sposób w liczbie ruchów 3, 4, 5, 6, 7, 8, 9 jest odpowiednio: 1, 1, 2, 3, 5, 8, 13.
Wynika stąd, że w liczbie ruchów nie większej niż 9 można zawiązać 33 takie węzły, gdyż 1+1+2+3+5+8+13=33, 21 z nich zawiązuje się w nieparzystej, a 12 w parzystej liczbie ruchów.
Jak już wiemy, każdy z tych węzłów jest przedstawicielem jednej rodziny, z których pozostałe otrzymuje się zamieniając operacje S na S*.
Podano je w § 5.
Dla przykładu, rodzina windsor, to
- S + ½O + S + W, czyli główny jej reprezentant,
- S* + ½O + S + W, wersja zwana węzłem perskim,
- S + ½O + S* + W,
- S* + ½O + S* + W, czyli najbardziej chyba popularna wersja.
Węzły uznawane za estetyczne noszą nazwy, pozostałe są bezimienne.
Wszystkie węzły z jednej rodziny noszą tę samą nazwę.
Powszechnie znanym wyjątkiem są S + W oraz S* + W, czyli nicky i pratt. Niewielu jednak wie, że jedna z wersji windsora nazywana jest węzłem perskim.
4.2. Rodziny, a wszystkie węzły
Ogólnie, oznaczając przez
R(
n) liczbę rodzin węzłów, które zawiązuje się w
n ruchach,
zauważamy, że
R(n) = R(n-1) + R(n-2),
gdyż węzły zawiązywane w
n ruchach
otrzymujemy dodając S (2 ruchy) do węzłów wiązanych w
n-2 ruchach i ½O (1 ruch) do
wiązanych w
n-1 ruchach.
Zatem
R(3),
R(4),
R(5), ... , czyli 1, 1, 2, 3, 5, 8, 13, ..., jest ciągiem Fibonacci'ego.
Wszystkich węzłów jest oczywiście więcej niż rodzin, patrz np. rodzina windsor, która liczy 4 węzły. Oznaczając przez
W(
n) liczbę wszystkich węzłów zawiązywanych w
n ruchach zauważamy, że
W(n+1) = 2W(n-1)+W(n).
Ponadto
W(3)=
W(4)=1.
Zatem w 3, 4, 5, 6, 7, 8 i 9 ruchach można zawiązać 1, 1, 3, 5, 11, 21 i 43 węzły. W liczbie ruchów nie większej niż 9 można więc ich zawiązać 85, ponieważ 1+1+3+5+11+21+43=85.
Liczba rodzin węzłów możliwych do zawiązania w 10, 11 i 12 ruchach wynosi 21, 34 i 55. Rośnie więc ona bardzo szybko.
Liczba wszystkich węzłów, które można zawiązać w 10, 11 i 12 ruchach jest natomiast równa 85, 171 i 341. Narasta ona jeszcze szybciej. Z tego też względu ograniczamy się tutaj do 9 ruchów.

Podamy teraz tablice wszystkich rodzin węzłów, które można zawiązać w licznie ruchów nie większej niż 9.
Przypominamy, że przy stanie początkowym L⊝, liczba ruchów jest nieparzysta.
Dla stanu początkowego L⊕ jest ona parzysta.
Węzły uznawane za estetyczne posiadają nazwy, pozostałe sa bezimienne.
W tablicach podano w zasadzie głównych reprezentantów poszczególnych rodzin, tzn. węzły zawiązywanie przy pomocy operacji
½O, S oraz W.
Jest jednak kilka wyjątków.
Dla rodziny nr 2 podano wszystkie jej węzły (czyli 2), gdyż każdy z nich posiada własną nazwę (nicky i pratt znany także jako shelby).
W rodzinie nr 21, bardziej niż główny jej reprezentant, znana jest wersja zmodyfikowana o nazwie van vijk.
Podobnie rzecz się przedstawia z rodziną nr 30, czyli christensenem.
W rodzinie nr 24, obok victorii podano równie znanego alberta.
Liczba ruchów n nieparzysta
Stan początkowy L⊝ |
Liczba ruchów n parzysta
Stan początkowy L⊕ |
| Nr |
n |
Węzeł |
Nazwa |
| 22 |
4 |
½O + W |
prosty |
| 23 |
6 |
S + ½O + W |
|
| 24 |
6 |
1½O + W |
victoria |
| 1½O + W2 |
albert |
| 25 |
6 |
½O + S + W |
półwindsor |
| 26 |
8 |
2S + ½O + W |
|
| 27 |
8 |
S + ½O + S + W |
windsor |
| S* + ½O + S + W |
perski |
| 28 |
8 |
S + 1½O + W |
|
| 29 |
8 |
½O + 2S + W |
|
| 30 |
8 |
½O + S + O + W |
|
| ½O + S + O + W2 |
christensen |
| 31 |
8 |
O + S + ½O + W |
cavendish |
| 32 |
8 |
1½O + S + W |
|
| 33 |
8 |
2½O + W |
|

6. Węzeł jako trajektoria w przestrzeni stanów
Siedem stanów krawata można przedstawić graficznie jak na rys. 9. Każdy jest reprezentowany przez okrąg, przy którym znajduje odpowiedni symbol stanu.
Tworzą one tzw. przestrzeń stanów.
Wiązaniu krawata odpowiada przechodzenie on jednego stanu do drugiego. Scieżka, która powstaje w ten sposób nazywa się trajektorią.
Trajektorie węzłów wiązanych w nieparzystej liczbie ruchów zaczynają się w stanie L⊝ zanaczonym na niebiesko, parzystym - L⊕ zaznaczonym na czerwono.
Wszystkie kończą się w stanie K zaznaczonym na czarno.
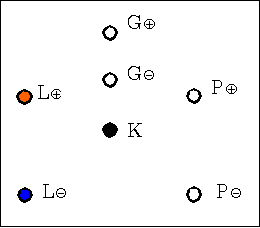
Rys. 9. Przestrzeń stanów
Trajektorie odpowiadające półwindsorowi i windsorowi pokazano na rys. 10.
Obie zaczynają się w w stanie L⊕, czyli w stanie oznaczonym na czerwono.
Trajektoria półwindsora przechodzi przez wszystkie stany, przez każdy tylko jeden raz.
Odpowiadająca windsorowi łączy wszystkie stany, pomiędzy którymi można przejść w jednym ruchu. (Zauważmy bowiem w tym miejscu, że nie każde dwa stany można połączyć jednym ruchem, np. L⊕ nie można połączyć z P⊕, tzn. nie można wykonać ruchu L⊕P⊕ ani P⊕L⊕.)
Pełna symetria jest w obu zakłócona przez jeden ruch, niejako brakujący lub nadmiarowy.
Niestety, całkowicie symetryczny węzeł nie istnieje.

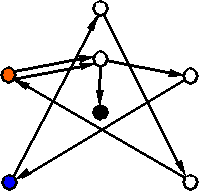
Rys. 10. Trajektorie półwindsora i windsora